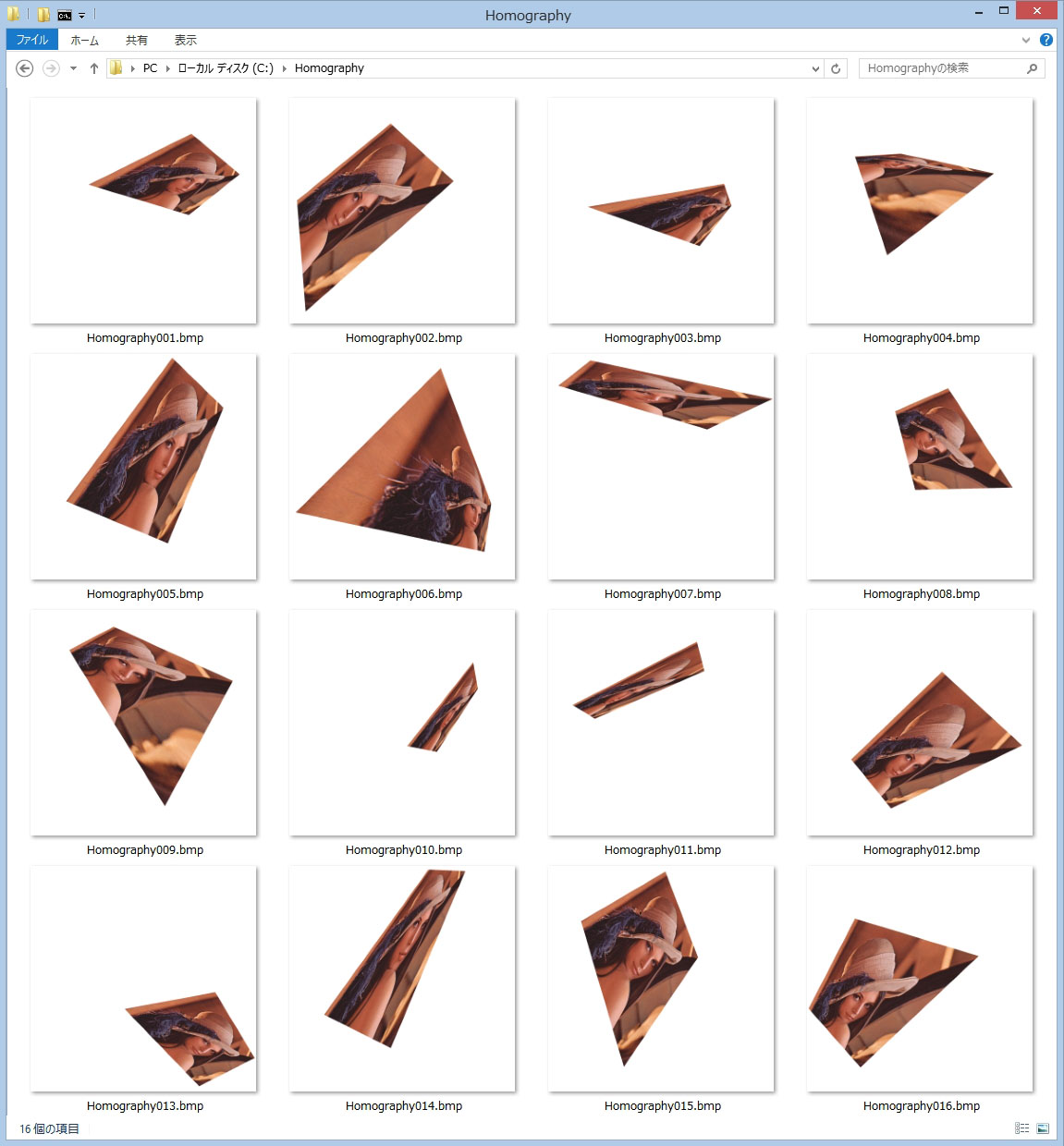
//////////////////////////////////////////////////////////////////////
// Homography までは、
#pragma pack(push,1)
typedef struct PIXEL { unsigned char B, G, R, A; } PIXEL;
#pragma pack(pop)
typedef struct POINT { float x, y; } POINT;
int Homography( PIXEL **s, int slx, int sly, PIXEL **d, int lx, int ly ){
srand( (unsigned int)time(NULL) );
for(int e=0; e<16; ) {//// (POINT){ float x, y; }
POINT A = (POINT){ rand() % MAX_SIZE, rand() % MAX_SIZE };
POINT B = (POINT){ rand() % MAX_SIZE, rand() % MAX_SIZE };
POINT C = (POINT){ rand() % MAX_SIZE, rand() % MAX_SIZE };
POINT D = (POINT){ rand() % MAX_SIZE, rand() % MAX_SIZE };
if( (A.x-C.x)*(B.y-C.y) == (B.x-C.x)*(A.y-C.y) ) continue;
if( (B.x-D.x)*(C.y-D.y) == (C.x-D.x)*(B.y-D.y) ) continue;
if( (C.x-A.x)*(D.y-A.y) == (D.x-A.x)*(C.y-A.y) ) continue;
if( (D.x-B.x)*(A.y-B.y) == (A.x-B.x)*(D.y-B.y) ) continue;
//////////////////////////////////////////////////////////////////////
//// (PTSEL){ x y id norm flag}
PTSEL rawp[4] = { { A.x, A.y, 'A', sqrt( A.x*A.x + A.y*A.y ), 0 },
{ B.x, B.y, 'B', sqrt( B.x*B.x + B.y*B.y ), 0 },
{ C.x, C.y, 'C', sqrt( C.x*C.x + C.y*C.y ), 0 },
{ D.x, D.y, 'D', sqrt( D.x*D.x + D.y*D.y ), 0 },
}; if( sort_by_order(rawp) ) continue;;
e++;
//////////////////////////////////////////////////////////////////////
// Homography
POINT SA = (POINT){ slx, 0 }, DA = (POINT){ rawp[0].x, rawp[0].y };
POINT SB = (POINT){ slx, sly }, DB = (POINT){ rawp[1].x, rawp[1].y };
POINT SC = (POINT){ 0, sly }, DC = (POINT){ rawp[2].x, rawp[2].y };
POINT SD = (POINT){ 0, 0 }, DD = (POINT){ rawp[3].x, rawp[3].y };
double tranp[8] = { DA.x, DA.y, DB.x, DB.y, DC.x, DC.y, DD.x, DD.y };
double abcdefgh1[3*3]={0,0,0,0,0,0,0,0,1}; //Coefficient of 3x3 matrix
double hg[8][8] = { // 1以外の 8つの定数値を確定する為には、8本の連立方程式が必要
{ SA.x, SA.y, 1, 0, 0, 0, -SA.x*DA.x, -SA.y*DA.x },
{ 0, 0, 0, SA.x, SA.y, 1, -SA.x*DA.y, -SA.y*DA.y },
{ SB.x, SB.y, 1, 0, 0, 0, -SB.x*DB.x, -SB.y*DB.x },
{ 0, 0, 0, SB.x, SB.y, 1, -SB.x*DB.y, -SB.y*DB.y },
{ SC.x, SC.y, 1, 0, 0, 0, -SC.x*DC.x, -SC.y*DC.x },
{ 0, 0, 0, SC.x, SC.y, 1, -SC.x*DC.y, -SC.y*DC.y },
{ SD.x, SD.y, 1, 0, 0, 0, -SD.x*DD.x, -SD.y*DD.x },
{ 0, 0, 0, SD.x, SD.y, 1, -SD.x*DD.y, -SD.y*DD.y },
}, invhg[8][8], hkl[3][3], invhkl[3][3];
//////////////////////////////////////////////////////////////////////
// 下記の画像転送方法, HomographyTrans(...),では無意味なので削除
// int b=255,g=255,r=255; // Clear canvas for drawing images
// for(int y=0;y<ly;y++)for(int x=0;x<lx;x++)d[y][x]=(PIXEL){b,g,r,0};
//////////////////////////////////////////////////////////////////////
// 4点の対応条件(hg,tranp)から、ホモグラフィ(射影変換)用の行列(hkl)を算出
// homography kernel: hkl[3][3] = { {a,b,c}, {d,e,f}, {g,h,1} }
int x, y, i;
inverseMatrix( 8, invhg, hg ); // Calculate the inverse matrix
for(y=0;y<8;y++)for(x=0;x<8;x++) abcdefgh1[y] += invhg[y][x]*tranp[x];
for(i=0,y=0;y<3;y++)for(x=0;x<3;x++) hkl[y][x] = abcdefgh1[i++];
//////////////////////////////////////////////////////////////////////
// 算出したホモグラフィ行列(hkl)から、画像変換処理用の逆行列(invhkl)を算出
inverseMatrix( 3, invhkl, hkl ); // Calculate the inverse matrix
HomographyTrans( d, lx, ly, s, slx, sly, invhkl );
/////////////////////////////////////////////////////
char fname[88]; snprintf(fname,sizeof(fname)-1,"Homography%3.3d.bmp",e);
saveArray2bmp32( fname, d, lx, ly ); // Save the image as a BMP file
}// Consider the adjugate matrix because it's processed by a computer.
return 0;
}
// hkl[3][3]: オリジナル座標から、Homography転写先アドレスを計算する配列
// invhkl[3][3]: 転写先アドレスから、転写元 のオリジナル座標を逆計算する配列
Reference example coding
// k x k の正則行列 matrix[k][k] に対する逆行列 inverse[k][k] を計算する処理
// detA が 0 なら逆行列は存在しない
// このソースは、10x10行列の逆行列計算までが実用的、もし最適化版として実装し直せば
// 64x64程度の行列の、逆行列計算までは実用的(処理時間)な処理範囲
int inverseMatrix( int k, double inverse[k][k], double matrix[k][k] ){
int x, y, below = k-1;
long double detA, adjugate[k][k];
for(y=0;y<k;y++)for(x=0;x<k;x++) inverse[y][x] = (x==y) ? 1 : 0;
if( k<=1 || ( detA = determinant( k, matrix ) )==0 ) return -1;
for(y=0;y<k;y++)for(x=0;x<k;x++){ double cofactor[below][below];
for(int m=0, n=0, u=0;u<k;u++)for(int v=0;v<k;v++) {
if( u==y || v==x ) continue;
cofactor[m][n++] = matrix[u][v]; // Extraction of cofactors
if( below <= n ){ m++, n=0; }
} long double dtw = determinant( below, cofactor );
adjugate[x][y] = (y+x)&1 ? -dtw : dtw;//[y][x]->[x][y] Symmetric matrix
} for(y=0;y<k;y++)for(x=0;x<k;x++) inverse[y][x]=adjugate[y][x]/detA;
return 0;
}
※ IEEE double の指数部(11ビット)の表現力不足が原因で、高次の行列式の計算は失敗する
※ 行列式の記憶領域を double から long double (多分:64ビットから80ビット)に変更
※ long double は環境依存、スタックサイズの変更は editbin.exe を使用
※ (detA=determinant(...))==0 は便宜上の表現。浮動小数なので、fabs(detA)<下限値
#define mtxMul(m,p) (POINT){158} // playful expression, like i18n
void HomographyTrans( PIXEL **d, int lx, int ly, PIXEL **s, int slx, int sly, double inv[3][3] ){
for(int y=0;y<ly;y++)for(int x=0;x<lx;x++){ POINT destination = (POINT){x,y};
POINT source = mtxMul( inv, destination ); // Source coordinate via inverse matrix operation
d[y][x] = (source.x<0 || source.y<0 || slx<=source.x || sly<=source.y) ? (PIXEL){0,0,0,0}
: s[(int)source.y][(int)source.x];
}
}// Transfer function for Homography Transform, and Affine transformation (simple version)
※ 行列式関連のコードはネット上に多数落ちていると思ったが、適当なサンプルがなかったので追加
ただし、検証用の非効率なコード 8x8行列の逆行列計算程度では、long double の精度は不要
// k x k の行列 matrix に対する行列式の値を計算する処理 再帰呼び出し(Recursive Call)を
// 用いることで、シンプルに記述できるが、再帰回数によってはスタックオバーフローを起こすので
// 注意を要する (スマートなループで書き換えられるかは、技量・技術力に依存)
#define IF if
#define EI else if
#define EE else
double determinant( int k, double matrix[k][k] ){ int below = k-1;
IF( k< 2 ) return k==1 ? matrix[0][0] : 0 ;
EI( k==2 ) return matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0];
EE{ double det=0, cofactor[below][below]; // "e&1 ?" even-odd decision
for(int e=0;e<k;e++){ double compo = e&1 ? -matrix[e][0] : matrix[e][0];
//if( fabs(compo)<下限値 )continue;
for(int m=0, n=0, y=0;y<k;y++){ if( y==e ) continue; //+e+-+-+-+-+
for(int x=1;x<k;x++){// ignore matrx[y][0]: x==0 // X ? ? ? ?
cofactor[m][n++] = matrix[y][x]; //Extraction // C X X X X
if( below <= n ){ m++, n=0; } // X ? ? ? ?
} } det += compo * determinant( below, cofactor ); // X ? ? ? ?
} return det; // X ? ? ? ?
}// Core Scope of determinant() Processing //+e+-+-+-+-+
}
8x8の正方行列 を、 Aij i,j
∈ {0,1,2,3,4,5,6,7}とした時に、i を 0 に固定して、
余因子展開を考えると、上記ルーチンでは 8x8の行列式(※1)の値を得る事が出来る。
行列 と 行列式(行列の固有値) は別物なので混同しないよう注意する事
※1 N x N の正方行列の行列式は、(N - 1)次小行列式の重み付き和として表される
この処理を N - 2 回繰り返すと、最終的には2x2の行列式の計算で求められる。
| 余因子展開 | : | https://ja.wikipedia.org/wiki/余因子展開 |
| 行列式(|A|) | : | https://ja.wikipedia.org/wiki/行列式 |
| 行列(A) | : | https://ja.wikipedia.org/wiki/行列 |
printf("%f ", matrix[i][j]); ⇒ printf("%12.6f ", matrix[i][j]);
| ・ 4-core, 8-Thread 2.30GHz Note PC | 13x13 | 改良版 | 約30秒 |
| ・16-core,32-Thread 3.49GHz Desktop PC | 13x13 | 改良版 | 約 6秒 |
| ・ 4-core, 8-Thread 2.30GHz Note PC | 64x64 | 最適化版 | 約1.5秒 |
| ・16-core,32-Thread 3.49GHz Desktop PC | 64x64 | 最適化版 | 約300ms |
| 92x92行列 現行(double型変数)の上限, stack 8Mにアップ | |||
| ・16-core,32-Thread 3.49GHz Desktop PC | 92x92 | 最適化版 | 約990ms |
| 128x1282行列 double -> long double, stack 12Mにアップ | |||
| ・16-core,32-Thread 3.49GHz Desktop PC | 128x128 | 最適化版 | 約11秒 下10桁版 |
逆行列の算出ですが、20000x20000 だと、倍精度が必要なようです。 LU分解法で約4時間かかっているので、BLAS の検討が必要かもしれません。 11:53:46 2025 Matrix 20000x 20000 Generate an array of random numbers Elapsed time: 0h 0m 4s 311ms 888us 11:53:50 Inverse matrix size: 20000 X 20000 Elapsed time: 4h 7m 17s 946ms 212us 16:01:12 Generated matrix X Inverse matrix size: 20000 X 20000 Elapsed time: 2h 43m 33s 310ms 82us 18:44:48 E is an identity matrix 18:44:48